記錄學習內容。看網路上大大們的文章和影片，做些紀錄。
以下內容大多來自網路上大大們的文章。截圖也來自文章和影片。
還不了解，內容可能有錯誤。

前面有大概了解了Minimum Spanning Tree :

就是 在一個圖中 ，選取這個圖 的所有點 ， 然後這些點要相連成一棵樹。
這棵樹 的 wight 總和 要是最小值 。
Minimum Spanning Tree 在一個圖中 可能不只一個 。

來學Kruskals Algorithms:

3.5 Prims and Kruskals Algorithms - Greedy Method(截圖來自教學)

Kruskal's Spanning Tree Algorithm
(截圖來自教學)

Kruskal’s Minimum Spanning Tree Algorithm
https://www.geeksforgeeks.org/kruskals-minimum-spanning-tree-algorithm-greedy-algo-2/
(截圖來自教學)

Kruskal's Spanning Tree Algorithm步驟 :
(最直覺的Minimum Spanning Tree 演算法 )

1
Remove 自己 連自己 的路線 。 因為自己連自己 就不算 樹了 。

2
把邊長 從 小 到 大 排列

3
就一個 一個 把 邊長 加入 樹中 。
然後 忽略 會形成圈圈(circuit、cycle) 的 路線

要判斷圈圈的部分 ，先看 :
Disjoint Set (Or Union-Find) | Set 1 (Detect Cycle in an Undirected Graph)
Union Find - Union and Find Operations

怎麼知道 這是一個 cycle ?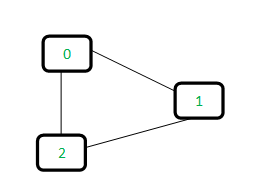

假設每個數字都有1個Subset (子集合?，想成一個數字一個袋子比較好理解)

一開始寫成這樣 ， -1代表 每個數字 自己都有一個袋子 
0   1   2
-1 -1  -1 

接著 邊長 開始判斷 ，像是 0 ->1 ，我們 就把 0放到1 的袋子，
所以現在 0 號  和 1號 都在  1號的袋子 。
寫成這樣:
0   1   2  
1  -1  -1
(0號 放到1 號的袋子 ，1號 還是在自己的袋子)

接著 邊長 1 到 2 :
變成這樣:
0   1   2  
1   2  -1
(1號 放到2號的袋子 ，2號 還是在自己的袋子)

接著邊長  邊長 0 到 2 :
變成這樣:
0   1   2  
2   2  -1
(0號 放到2號的袋子 ，2號 還是在自己的袋子)

所以現在 0號1號2號 都在2 號的袋子 ，代表這三個點 形成一個圈圈。
這樣就算 一個 cycle 了 。

來看 文章中的程式怎麼寫的。

Parent[] 就是袋子 ，每個點都有一個專屬的袋子 (-1)。
然後就開始 一個邊、 一個邊 檢查 。
像是 現在 0 號 到1號 的邊
Src 代表0 號
Dst 代表 1號
如果 Src 和 Dst 的袋子 是同一個 ，代表 現在這兩個號碼 ，都在另一個袋子
， 代表現在某個袋子有三個號碼 。 三個號碼 就會 形成 1個圈圈 。
如果 Src 和 Dst 的袋子 是不同的 。代表 我們 要把 這兩個號碼 ，都裝到其中一個號碼的袋子

來看 如何 把 兩個號碼放到 同一個袋子 。(Union 聯集):

如果袋子的值是 -1 ，就代表 是自己的袋子 。
如果 parent[1] = 5 。就代表 去到5號檢查， 如果5號 是 -1 就代表
5 號 在自己的袋子 ，如果不是-1 ，就代表 要在繼續尋找袋子(父母) 。

可能還是不太懂 ，不過就在回到Kruskal's algorithm 演算法

步驟1 :先排序邊長
步驟2 :創建subset ，排序，代表每個點都有自己的袋子
步驟3 : 開始迴圈 ，
如果 邊長的兩個點 是相同袋子的話，就代表會形成cycle。所以忽略。
如果 邊長的兩個點 ，是不同的就代表 要進行Union

Union 這邊的程式:
用了rank來判斷要分哪邊

為什麼要用rank，因為會發生這種狀況:
不知道是C接到A ，還是A接到C 。所以要接到個數比較多，rank比較大的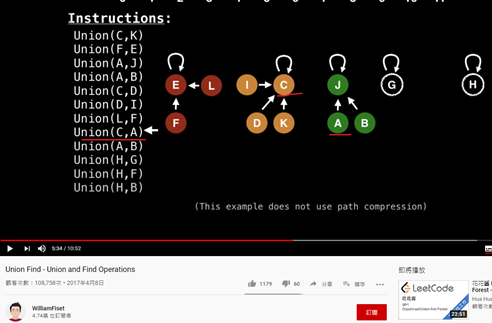

來看時間複雜度:
簡單記法，因為會走訪每條邊 ，所以前面是E。
每條邊都要取Union(聯集)，聯集要找父母。找袋子，有關樹往上爬的時間複雜度
大概都是logV
所以就是E 乘 logV

更新時間複雜度，引用最後一段:
https://www.geeksforgeeks.org/kruskals-minimum-spanning-tree-algorithm-greedy-algo-2/

Time Complexity: O(ElogE) or O(ElogV). Sorting of edges takes O(ELogE) time. After sorting, we iterate through all edges and apply find-union algorithm. The find and union operations can take atmost O(LogV) time. So overall complexity is O(ELogE + ELogV) time. The value of E can be atmost O(V2), so O(LogV) are O(LogE) same. Therefore, overall time complexity is O(ElogE) or O(ElogV)

空間複雜度 就是 點和邊